안녕하세요 이번 포스팅은 오차를 계산해서 이상적인 모델을 도출하는 경사 하강법에 대해서 설명드리도록 하겠습니다. 물론 이 방법도 선형 회귀 방법을 하는 과정에서 오차를 줄여가면서 이상적인 모델의 기울기와 y 절편을 구하는 방법입니다.
경사 하강법
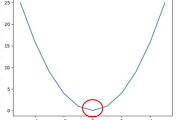
: 경사 하강법은 임의의 기울기를 잡고 구했을 때는 오차 값이 큰 단점을 보완하기 위해 임의의 기울기와 y 절편을 대입했을 때 발생하는 오차에 대해서 검토를 해보고 그 오차를 최소한으로 줄이는 방법으로 이상적인 모델을 구축할 수 있는 기울기 "a"와 y절편을 구하는 방법입니다. 그리고 여기에서는 추가적으로 인지를 하셔야 하는 게 오차와 기울기의 2차 함수 곡선에서 기울기가 "0" 일 때의 오차 값을 구하는 것입니다. 아래 그림을 보시면 맨 아래 기울기가 "0" 지점이 올 때까지 계속적으로 계산을 하는 것입니다.
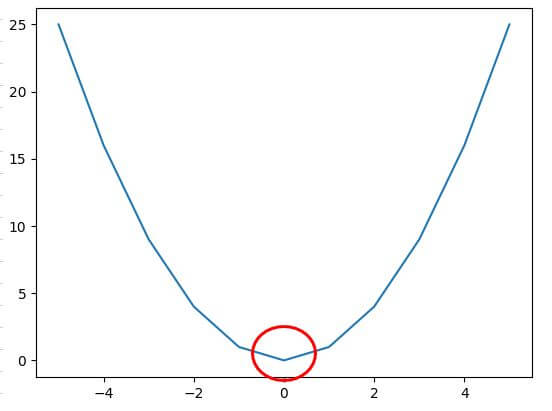
▼ 위의 오차와 기울기의 이차 함수 그래프에서 기울기가 "0" 이 될 때 나오는 모델의 기울기와 y절편을 구하는 것을 반복적인 수식이 아닌 파이썬 코드를 통해서 구현을 하려고 합니다.
경사 하강법 코드 구현
: 위에 설명드렸던 경사 하강법의 개념을 이용하여 코드를 구현해보도록 하겠습니다. 일단 기존에 작성한 평균 제곱 오차 공식에서 이용한 Source Data를 이용하여 코드를 구현해보도록 하겠습니다.
▼ 혹 평균 제곱 오차 공식에 대한 포스팅을 보지 않으셨다면 아래 링크 확인하시면 될 거 같습니다.
Python 딥러닝 선형 회귀 평균 제곱 오차
안녕하세요 이번 포스팅은 선형 회귀 방법을 이용하기 위한 평균 제곱 오차에 대해서 설명 드리도록 하겠습니다. 평균 제곱 오차의 경우에는 딥러닝을 위해서 오차를 구해야 하는데 이때 사용
davey.tistory.com
여기에서 추가적으로 적용해야 하는 게 학습률인데, 오차를 계산하고 그것을 제곱한 값에 대해서 어느 정도를 반영하여 기존에 설정한 기울기와 y절편에 반영을 할 건지에 대한 Factor입니다. 말로 표현을 하니까 아래 코드를 통해서 도출한 수식과 함께 설명드리도록 하겠습니다.
# 필요한 라이브러리를 선언
import numpy as np
import matplotlib.pyplot as plt
# 기존에 평균 제곱 오차 공식에서 사용한 Source Data
T_W = [10, 20, 30, 40,50]
Math_Score = [80, 85, 70, 99, 90]
# 추가적으로 다른 형태로 리스트를 표현하는 방식임. 참조하세요.
T_W_R = [i for i in T_W]
Math_Score_R = [i for i in Math_Score]
# 리스트 함수를 배열 함수로 표현하는 방법
x_axis_data = np.array(T_W_R)
y_axis_data = np.array(Math_Score_R)
# 모델 구하는 작업을 몇번 할 지를 설정
epochs = 2001
# 모델 구하는 공식에 학습률을 설정
R_rate = 0.001
# 초기 임의의 a, b 값을 설정
a = 0
b = 0
# 아래 수식을 통해서 a, b 의 이상적인 값을 도출
for i in range(epochs):
predict_value = a * x_axis_data + b
difference = y_axis_data - predict_value
a_diff = - (2/len(x_axis_data) * sum(x_axis_data * difference))
b_diff = - (2/len(x_axis_data) * sum(difference))
a = a - R_rate * a_diff
b = b - R_rate * b_diff
if i % 100 == 0:
print("No of Execution =%.01f, 기울기(a) =%.03f, y 절편(b) %.03f" % (i,a,b))
# 모든 과정이 끝난 최종 예상값을 출력
print("y_pred result = ", predict_value)
print("x_data 값 = ", x_axis_data)
# 최종으로 구한 a, b 값을 이용하여 모델을 설정
# 해당 모델에 대해서 이전 Source 값과 예상값을 그래프로 출력
y_pred = a * x_axis_data + b
plt.scatter(x_axis_data,y_axis_data)
plt.plot([min(x_axis_data), max(x_axis_data)],[min(predict_value), max(predict_value)])
plt.show()
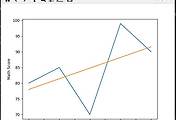
▼ 위 코드에서 For 문에 들어 있는 수식이 모델의 a와 b 즉, 기울기와 y 절편을 구하는 식이라고 생각하시면 됩니다. 그리고 이런 모델을 설정하고 그 모델에 맞춰서 동일한 x_axis_data에 맞춰서 기존에 y_axis_data와 새로운 결괏값을 비교하는 그래프를 보여 줄 수 있습니다. 위 코드를 실행을 해보면 아래와 같은 결과 값을 보실 수 있습니다.
# 수정된 모델을 통해서 출력된 y 값
y_pred result = [-8.37186291e+160 -1.67209518e+161 -2.50700407e+161 -3.34191296e+161
-4.17682185e+161]
x_data 값 = [10 20 30 40 50]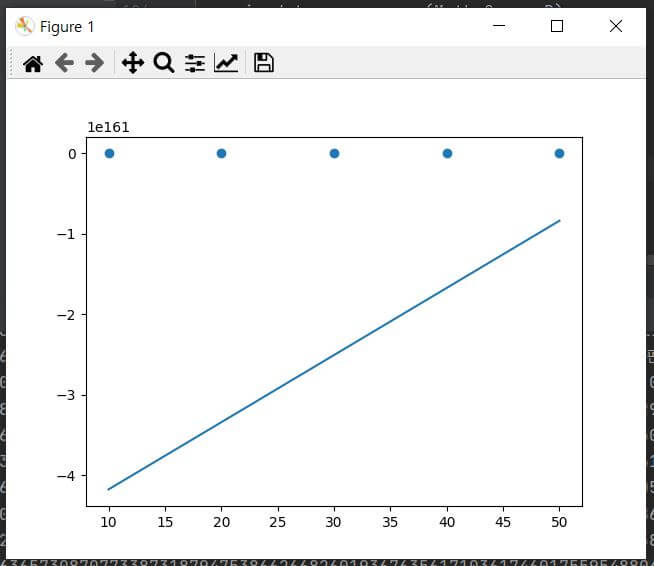
위 출력되는 결과와 그래프를 보시면 정말 너무나도 차이가 나는 출력값이 도출되는 것을 발견하실 수 있습니다. 심지어 학습률을 조금만 키워도 오버 플로우(오차 값을 통해서 모델을 추출하는 과정에서 벗어나는 현상) 생기게 됩니다. 즉 여기에서 얻을 수 있는 교훈은 Source Data에 맞춰서 적당하게 모델 기울기와 y절편을 설정을 해야 하는 것입니다. 터무니없게 생각도 안 하고 설정하게 되면 이런 결과가 나오게 됩니다.
▼ 그래서 학습률은 그대로 나두고, Source Data를 약간 수정해서 다시 코드를 구현해보았습니다. 수정된 Source Data는 아래와 같습니다.
# x_axis_data를 너무 크지 않게 수정함.
T_W = [2, 4, 6, 8,10]
Math_Score = [81, 93, 91, 97, 99]
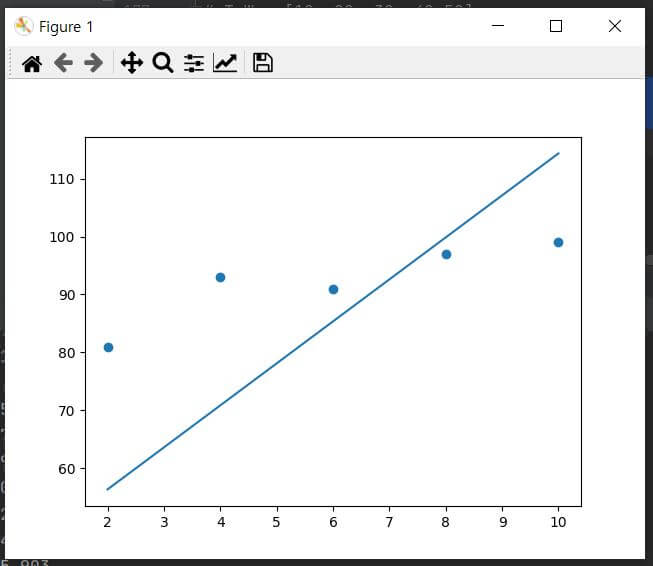
아래 그래프와 결과 값을 보시면 그래도 나름 구현이 가능한 결과 갑과 그래프가 도출이 되는 걸 확인하실 수 있습니다. 여기에서 얻는 교훈은 정말 초기 값과 학습률을 Source Data에 맞게 잘 설정을 해야 한다는 것입니다.
# Source Data 수정 후 도출 된 y 값
y_pred result = [ 56.30416579 70.82377864 85.34339149 99.86300433 114.38261718]
x_data 값 = [ 2 4 6 8 10]
이상입니다. 지금까지 오차를 계산해서 이상적인 모델을 도출하는 경사 하강법에 대해서 포스팅을 작성하였습니다. 초기값, 학습률을 Source Data를 잘 파악하지 못하고 적용하게 되면 오버 플로우 같은 현상이 발생할 수도 있으니 이 점 참조하시고 코드를 구현을 하셨으면 합니다. 제 포스팅인 경사 하강법을 이해하시는데 도움이 되었으면 합니다. 이만 마무리하도록 하겠습니다. 감사합니다.
[저작권이나, 권리를 침해한 사항이 있으면 언제든지 Comment 부탁드립니다. 검토 후 수정 및 삭제 조치하도록 하겠습니다. 그리고, 기재되는 내용은 개인적으로 습득한 내용이므로, 혹 오류가 발생할 수 있을 가능성이 있으므로, 기재된 내용은 참조용으로만 봐주시길 바랍니다. 게시물에, 오류가 있을 때도, Comment 달아 주시면, 검증 결과를 통해, 수정하도록 하겠습니다.]
관련 다른 글
'파이썬 (Python) > 딥러닝 (Deep Learning)' 카테고리의 다른 글
| Python 딥러닝 로지스틱 회귀 (시그모이드 함수) (0) | 2021.06.12 |
|---|---|
| Python 딥러닝 다중 선형 회귀 경사 하강법 (1) | 2021.06.10 |
| Python 딥러닝 선형 회귀 평균 제곱 오차 (0) | 2021.06.05 |
| Python 딥러닝 선형 회귀 최소 제곱법 구현 해보기 (0) | 2021.06.04 |
| Python opencv 이용하여 채널 분리 및 병합하는 방법 (0) | 2021.03.17 |

댓글