안녕하세요 이번 포스팅은 Python에서 딥러닝에 사용하는 방법인 선형 회귀에 이어 로지스틱 회귀에 대해서 설명 및 코드를 구현을 통해서 어떻게 딥러닝을 하는지에 대해서 설명드리도록 하겠습니다. 오차 함수 및 지수 함수 그리고 시그모이드 함수를 사용할 예정입니다.
로지스틱 회귀
: 로지스틱 회귀에 대해서 먼저 설명 드리도록 하겠습니다. 간단하게 말씀드리면 합격 불합격과 같이 바로 결과가 나오는 방식을 로지스틱 회귀라고 합니다. 예를 들어 공부하는 시간이 2, 4 시간 일 때 4시간인 경우에는 합격하고 2시간에는 불합격하는 데이터를 머신러닝을 시켜 놓으면 어떤 학생이 2시간을 공부했다고 입력을 집어넣으면 불합격할 거라고 결과가 나오는 것입니다.
▼ 물론 데이터가 작으면 작을 수록 모델에서 출력하는 결과는 한정이 있을 겁니다. 이런 데이터를 여러 개를 해서 입력 데이터에 따라 최적의 출력 값을 뽑아 주는 게 목적인 방식입니다.
합격 불합격의 간단한 사례를 이용해서 그래프를 그려보면 아래와 같습니다. 즉 위에 위치한 Value가 "1"인 라인은 합격을 나타내는 것이고, 아래 "0"을 나타내는 것은 불합격을 의미합니다. Source Data와 함께 첨부하도록 하겠습니다.
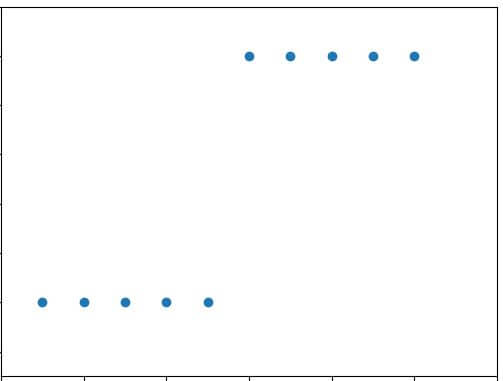
아래 Source Data를 보시면 아시겠지만 일단 x_data의 경우에는 공부하는 시간이고, y_data는 합격 불합격을 알려주는 Value입니다. "0" or "1"인 것입니다. 그런데 리스트 안에 리스트가 있으니까 추가적으로 따로 리스트를 분리하는 작업을 해준 것입니다. 그래서 좀 더 쉽게 이해하시라고 아래와 같이 따로 리스트를 분리를 해도 똑같은 입력값을 준비할 수 있다는 것을 말씀드린 것입니다.
▼ 추가적인 for 문을 이용한 리스트화는 이런 형태로도 for문을 사용할 수 있다는 점을 알려드릴려고 중복으로 기재한 내용이니 연습을 해보시는 걸 추천드립니다.
# 필요한 라이브러리를 선언
import numpy as np
# 공부하는 시간에 맞춰서 합격하는 확률
# 각 리스트에 안에 있는 리스트 첫번째 value가 공부시간, 그리고 두번째 value가 합격 불합격 유무
data = [[1, 0], [2, 0], [3, 0], [4, 0], [5, 0], [6, 1], [7, 1], [8, 1], [9, 1], [10, 1]]
# 각 리스트에서 따로 별도의 리스트로 분리
x_data = [i[0] for i in data]
y_data = [i[1] for i in data]
# 위의 리스트 형태를 아래와 같이 표현해도 똑같은 Source 값임(참조요망)
data1 = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
data2 = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
x_data = [i for i in data1]
y_data = [i for i in data2]
#시그모이드함수를 위한 각 value의 배열화를 시키는 코드
x_data_revised = np.array(x_data)
y_data_revised = np.array(y_data)
시그모이드 함수
: 그럼 위에 설명드린 로지스틱 회귀 방식을 구현하기 위해서 시그모이드 함수를 사용해서 구현해보도록 하겠습니다. 시그모이드 함수의 수식은 y = 1 / e**(a * x_data + b)입니다. 로지스틱 회귀처럼 참과 거짓, 합격과 불합격과 같은 1, 0의 value를 가지고 표현하는데 유용하게 사용하는 함수라고 생각하시면 됩니다. 그럼 위에서 구현한 Source Data를 이용해서 시그모이드 함수를 이용한 로지스틱 회귀를 구현해보도록 하겠습니다.
일단 코드를 구현하기 위해서는 기울기와 y절편에 대한 초기값을 선언을 해야 합니다. 물론 이상적인 기울기와 y절편을 구하기 위해서 학습률도 정해줘야 합니다. 여기에서 질문이 들어올 것입니다. 그럼 이거는 어떻게 정해야 하느냐는 애기입니다.
▼ 여기에서 대답은 아무거나 집어넣으라는 것입니다. 하지만 학습률은 over flow 생기기 않게 일단 0.1 or 0.01 단계에서 시작을 하시면 될 거 같습니다. 그리고 학습 횟수도 1000 단위로 잡으시면 될 거 같습니다. 즉 답은 없고, 약간의 노가 대성이 필요한 작업입니다.
# 기울기와 y절편의 초기값을 "0" 으로 잡음
a = 0
b = 0
# 학습률을 선언
rate = 0.02
#학습할 횟수 선언
epochs = 4001
# 시그모이드 함수를 선언
def sigmoid_fomula(input):
return 1 / (1+ np.e**(-input))
# 선언한 시그모이드 함수를 학습할 횟수에 맞춰서 학습을 시키는 코드
for i in range(epochs):
for x_data, y_data in data:
a_difference1 = x_data*(sigmoid_fomula(a*x_data + b) - y_data)
b_difference2 = sigmoid_fomula(a*x_data + b) - y_data
a= a - rate * a_difference1
b= b - rate * b_difference2
# 500번 학습 할 때 마다 기울기와 y절편의 값을 출력
if i % 2000 == 0:
print("epoch=%.04f, 기울기 a =%.02f, y 절편 b =%.02f" % (i, a, b))
# 기존 Data를 점으로 표현하는 코드
plt.scatter(x_data_revised, y_data_revised)
#x,y의 범위를 아래와 같이 설정함
plt.xlim(0, 12)
plt.ylim(-.3, 1.2)
#학습한 모델에 입력하는 일정의 x 값을 설정하고 입력 후 그래프로 출력하는 코드
x_range = (np.arange(0, 12, 0.1))
plt.plot(np.arange(0, 12,0.1), np.array([sigmoid_fomula(a * x + b) for x in x_range]))
plt.show()
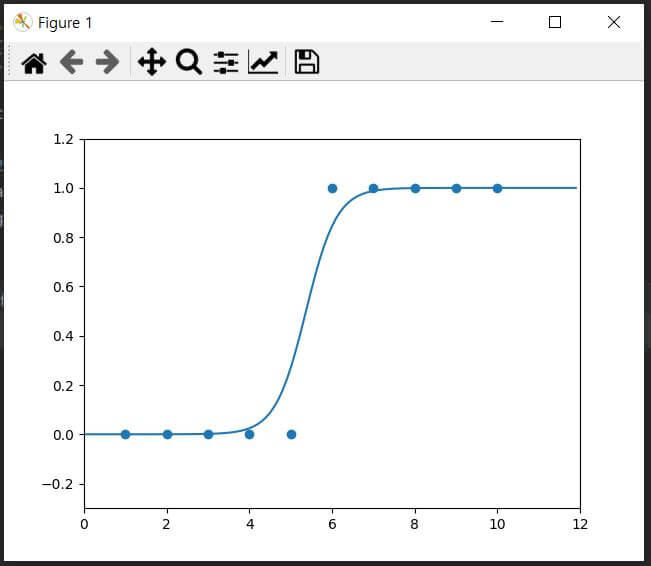
▼ 위 코드를 실행을 해보면 아래와 같이 출력 값이 출력이 되고 그래프가 출력이 되는 걸 확인하실 수 있습니다. 일단 x 값, input 값을 선형적으로 입력을 하였고 이것에 대한 결과 값이 선형적으로 나왔으니까 출력되는 출력 값과 그래프는 무난하게 나왔습니다. 하지만 좀 더 복잡하게 할 경우에는 출력 값과 그래프 값이 다르게 나올 수 있으니 이 점 참조하시면서 코드를 분석하고 구현하시길 추천드립니다.
epoch=0.0000, 기울기 a =-0.01, y 절편 b =-0.01
epoch=0.0000, 기울기 a =-0.03, y 절편 b =-0.02
epoch=0.0000, 기울기 a =-0.06, y 절편 b =-0.03
epoch=0.0000, 기울기 a =-0.09, y 절편 b =-0.04
epoch=0.0000, 기울기 a =-0.13, y 절편 b =-0.05
epoch=0.0000, 기울기 a =-0.05, y 절편 b =-0.03
epoch=0.0000, 기울기 a =0.04, y 절편 b =-0.02
epoch=0.0000, 기울기 a =0.10, y 절편 b =-0.01
epoch=0.0000, 기울기 a =0.16, y 절편 b =-0.01
epoch=0.0000, 기울기 a =0.19, y 절편 b =-0.00
epoch=2000.0000, 기울기 a =1.88, y 절편 b =-10.04
epoch=2000.0000, 기울기 a =1.88, y 절편 b =-10.04
epoch=2000.0000, 기울기 a =1.88, y 절편 b =-10.04
epoch=2000.0000, 기울기 a =1.87, y 절편 b =-10.04
epoch=2000.0000, 기울기 a =1.84, y 절편 b =-10.04
epoch=2000.0000, 기울기 a =1.87, y 절편 b =-10.04
epoch=2000.0000, 기울기 a =1.88, y 절편 b =-10.04
epoch=2000.0000, 기울기 a =1.88, y 절편 b =-10.04
epoch=2000.0000, 기울기 a =1.88, y 절편 b =-10.04
epoch=2000.0000, 기울기 a =1.88, y 절편 b =-10.04
epoch=4000.0000, 기울기 a =2.41, y 절편 b =-13.02
epoch=4000.0000, 기울기 a =2.41, y 절편 b =-13.02
epoch=4000.0000, 기울기 a =2.41, y 절편 b =-13.02
epoch=4000.0000, 기울기 a =2.41, y 절편 b =-13.02
epoch=4000.0000, 기울기 a =2.38, y 절편 b =-13.02
epoch=4000.0000, 기울기 a =2.41, y 절편 b =-13.02
epoch=4000.0000, 기울기 a =2.41, y 절편 b =-13.02
epoch=4000.0000, 기울기 a =2.41, y 절편 b =-13.02
epoch=4000.0000, 기울기 a =2.41, y 절편 b =-13.02
epoch=4000.0000, 기울기 a =2.41, y 절편 b =-13.02
이상입니다. 지금까지 Python에서 딥러닝에 사용하는 방법 중에 로지스틱 회귀에 대해서 설명 및 코드를 구현을 통해서 어떻게 딥러닝을 하는지에 대해서 설명드리도록 하겠습니다. 위에서 설명드린 것 중에 오차함수 및 지수 함수 그리고 시그모이드 함수를 섞어서 설명 드린 내용이니 이 부분에 대해서 기본 지식을 얻고 싶으시면 구글이나 네이버에서 검색하시면 자세히 나올 것입니다. 그럼 이만 마무리하도록 하겠습니다. 감사합니다.
관련 다른 글
'파이썬 (Python) > 딥러닝 (Deep Learning)' 카테고리의 다른 글
| Python 딥러닝 오차 역전파 고급 경사 하강법 (0) | 2021.06.22 |
|---|---|
| Python 딥러닝 퍼셉트론 이론 및 XOR 문제 해결 코드 구현 (0) | 2021.06.13 |
| Python 딥러닝 다중 선형 회귀 경사 하강법 (1) | 2021.06.10 |
| Python 딥러닝 경사 하강법 (0) | 2021.06.08 |
| Python 딥러닝 선형 회귀 평균 제곱 오차 (0) | 2021.06.05 |
댓글